本章学习内容
单向散列值函数可以获取消息的指纹。
这一章我们会接触不同的单向散列值函数:SHA-1、SHA-2、SHA-3
什么是单向散列函数
这个文件是不是真的?
我们经常需要判断文件是否被篡改,这种“是真的”性质是完整性,也叫做一致性。
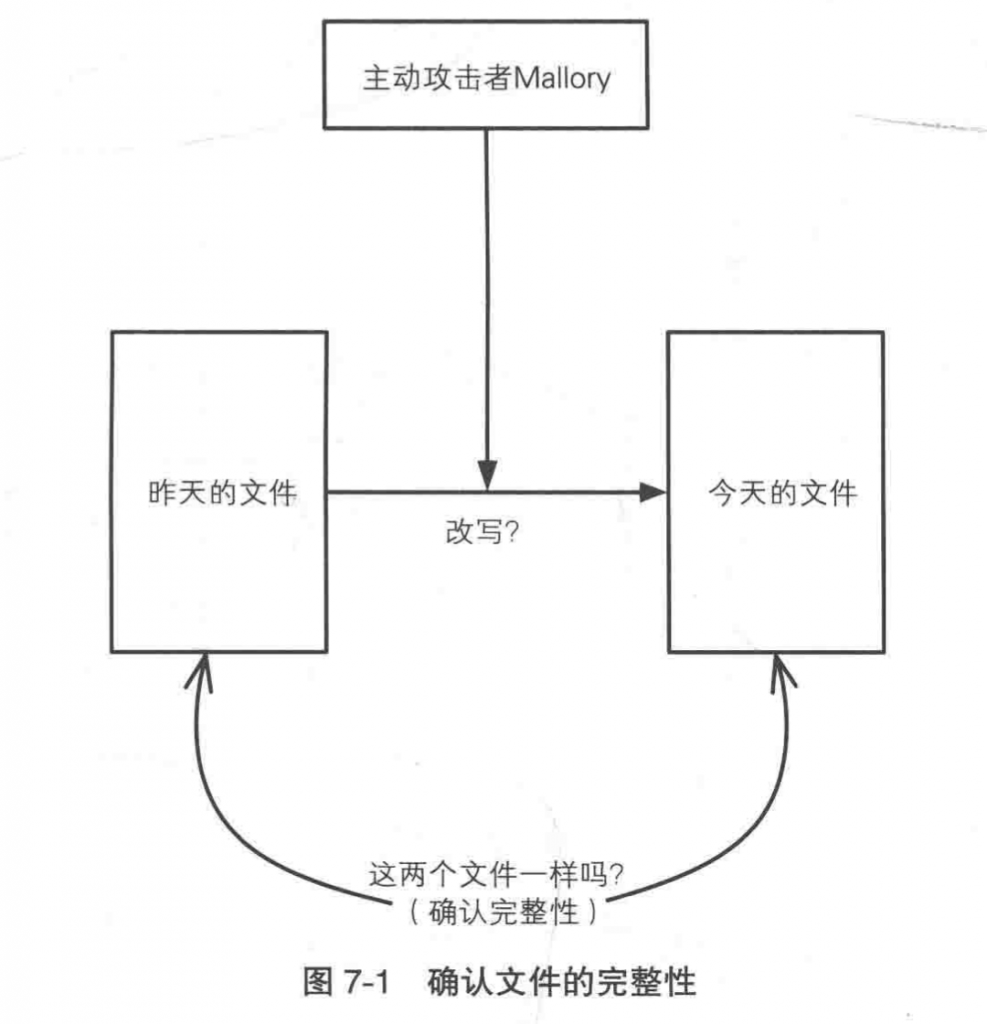
最初的方法可能是把文件保存下来,然后放到安全的地方,第二天再把这个文件和昨天的文件进行对比
文件在非常大的时候文件的复制、保存都是非常耗时的,我们需要获取指纹一样确认文件的完整性。
通过单向散列函数我们就可以做到上面我们说的事情。
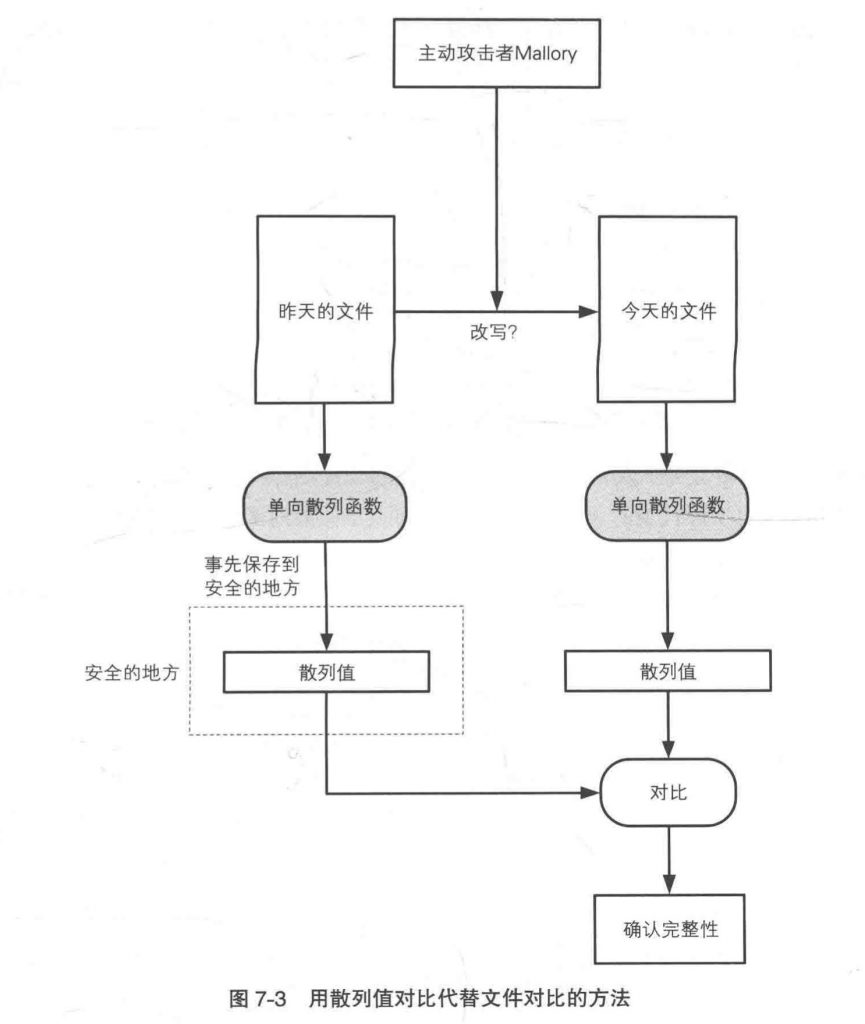
什么是单向散列函数
单向散列函数有一个输入以及一个输出,输入为消息而输出为散列值
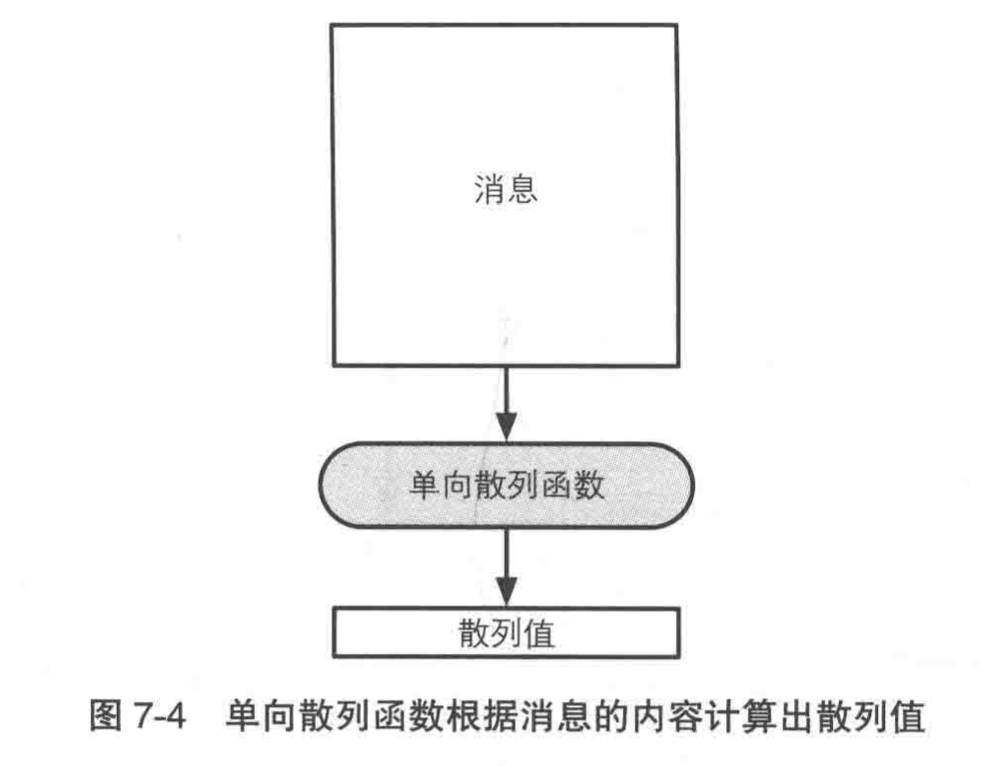
散列值可以将任意的消息,转换为相同长度的比特序列。
我们只要保证昨天算出来的散列值和今天算出来的散列值是一样的就可以保证文件是相同的。
单向散列函数的性质
根据任意长度的消息计算出固定长度的散列值
能够快速计算出散列值
消息不同散列值也不同
两个不同的消息产生一个散列值的情况被称为碰撞,单向单列值函数需要保证不可能被认为地发现碰撞。这种性质叫做抗碰撞性。
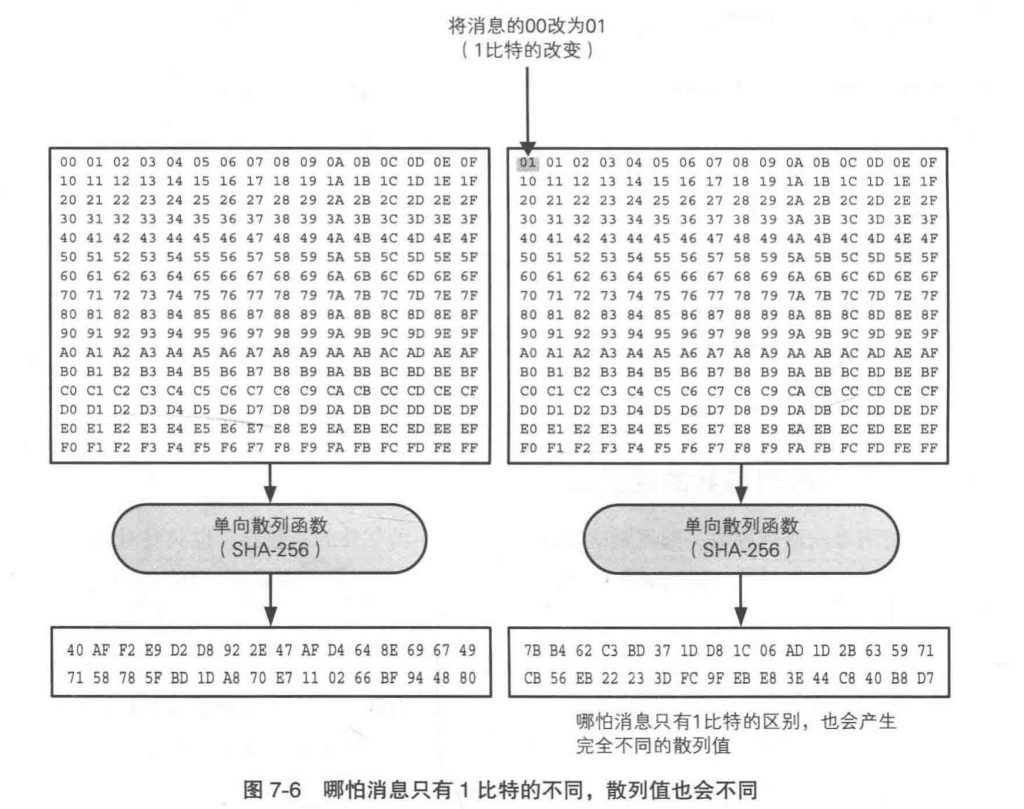
如果不能够抗碰撞,那么可能会被恶意地篡改信息而无法察觉。
这里有两个概念:
强抗碰撞性:要找到散列值相同的两条消息是非常困难的
弱抗碰撞性:要找到和该条消息有相同的散列值的另外一条消息是非常困难的
单向散列函数都必须具备弱碰撞性
具备单向性
无法通过散列值反算出消息的性质
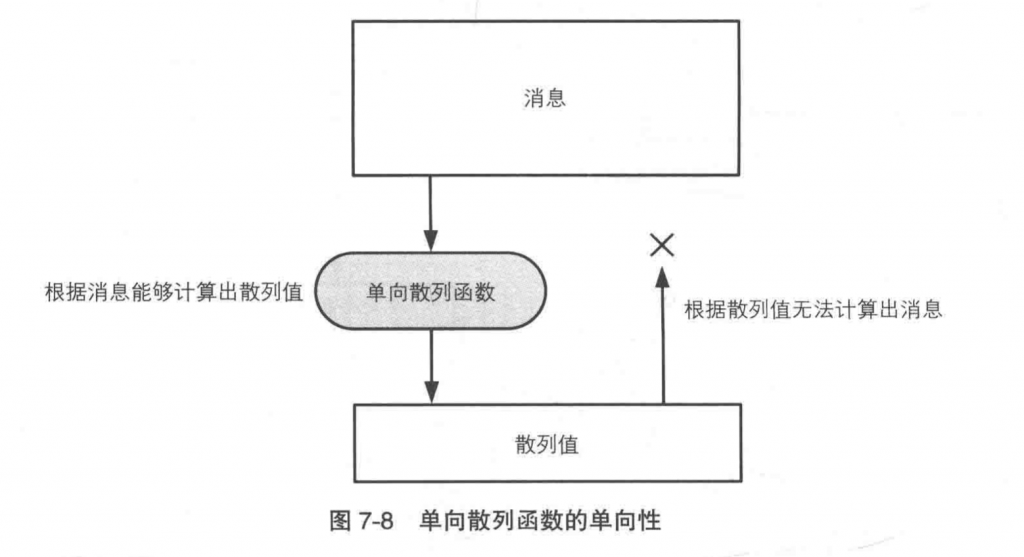
关于术语
单向散列函数也等价于消息摘要函数、哈希函数或者杂凑函数。
输入单向散列函数的消息也称为原像(pre-image)
单向散列函数输出的散列值被称为信息摘要或者指纹。
完整性也称为一致性
单向散列函数的应用
防止软件被篡改,镜像站点等
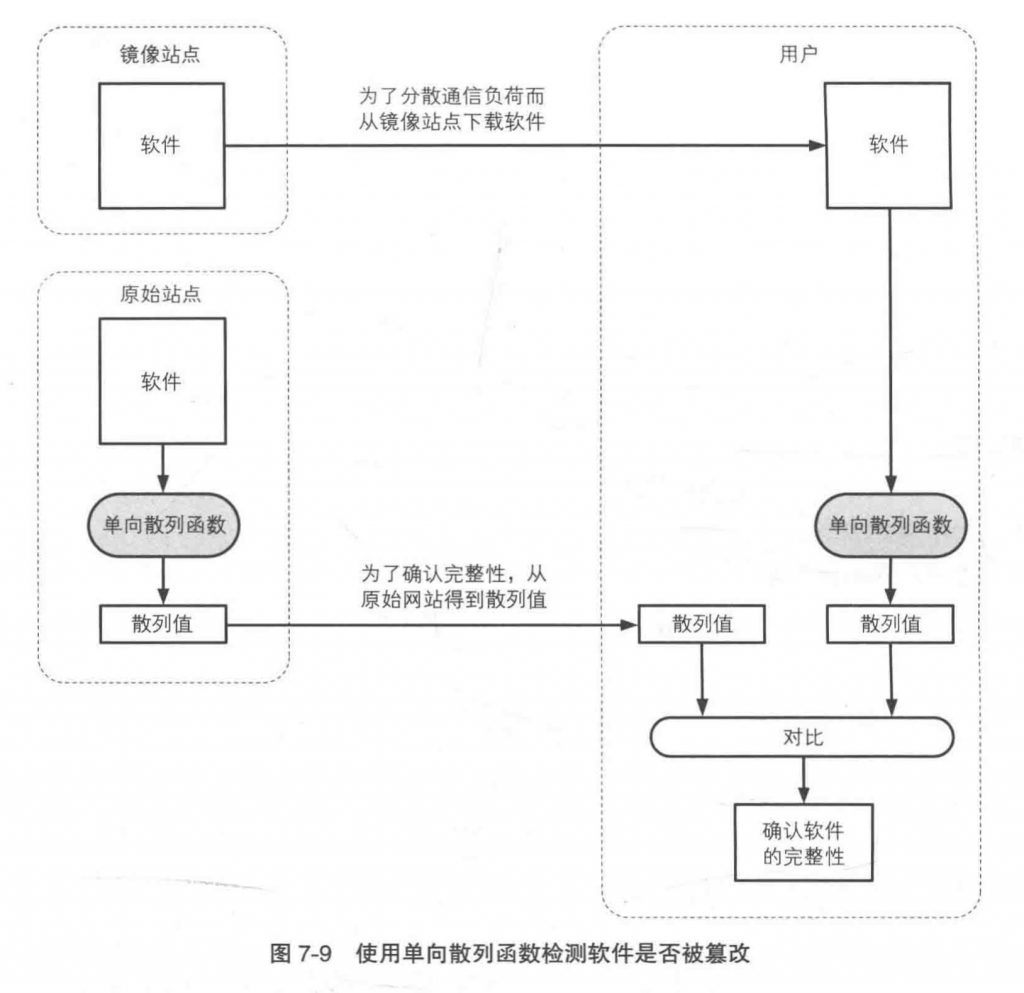
基于口令的加密
消息认证码
数字签名
伪随机数生成器
一次性口令
单向散列函数的例子
MD4、MD5
目前MD5的强抗碰撞性已经被打破,也就是说现在已经能够产生相同散列值的两条不同的消息,所以已经不安全了
SHA-1、SHA-256、SHA-384、SHA-512
SHA-1已经只用于保证兼容性的地方了,其强碰撞性被攻破。
SHA-2还未被攻破。
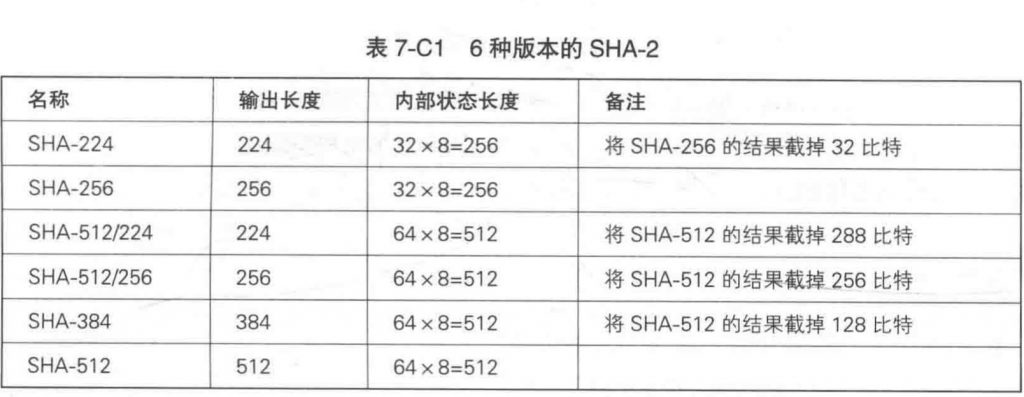
RIPEMD-160
RIPEMD强抗碰撞性已经被攻破,但是RIPEMD-160还未被攻破。比特币使用的就是RIPEMD-160。
SHA-3
SHA-3也是通过公开竞争的方式进行标准化的。一个名叫Keccak的算法胜出。
SHA-3的选拔过程
使用Keccak的理由如下:
- 采用了与SHA-2完全不同的结构
- 结构清晰易于分析
- 能够适用于各种设备,也适用于嵌入式
- 在硬件上的实现显示出了很高的性能
- 比其他候选算法的安全性边际更大
SHA-3最终候选名单
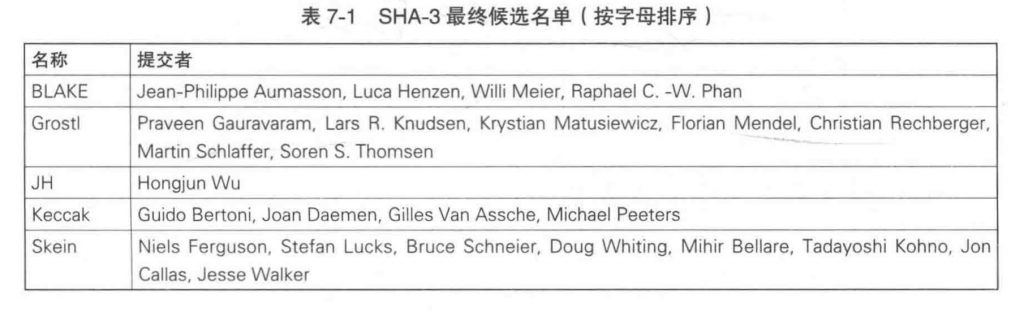
Keccak
什么是Keccak
Keccak可以生成任意长度的散列值,但是为了配合SHA-2的长度所以指定了部分长度的版本。
海绵结构
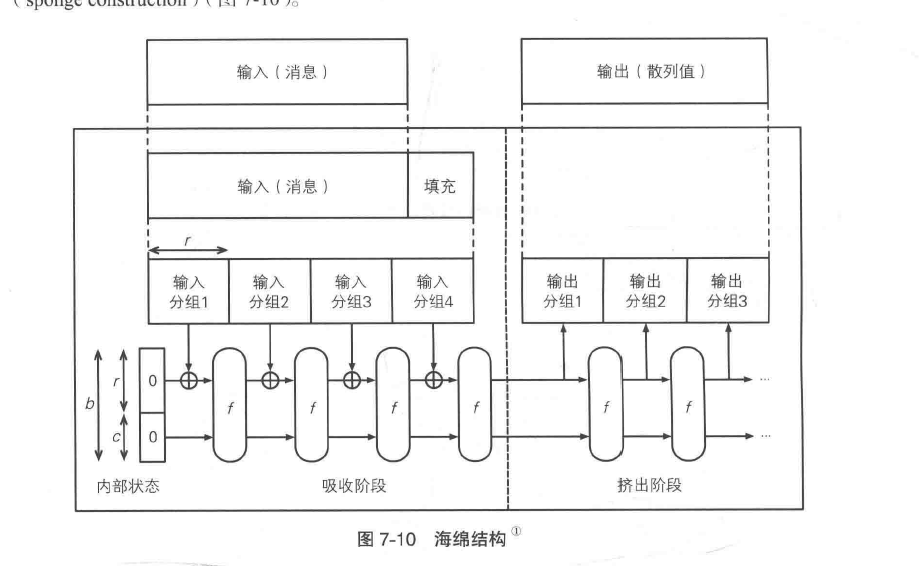
在输出数据进行填充之后要经过吸收阶段和挤出阶段
输入和输出长度为b,内部状态的c个比特是固定的,输入f的长度为r+c=b
c被称为容量,防止将输入信息的特征泄漏。
吸收阶段
- 先将经过填充的输入信息按照r比特切分
- 内部状态的r个比特与输入分组1进行XOR,然后输入函数f
- 函数f输出的r个比特与输入分组2进行XOR,然后再输入f
- 反复到最后一个分组
- 结束吸收阶段
挤出阶段
- 将函数f的输出的r比特作为输出分组1,并且将整个输出值(r+c)在此输入到f中
- 然后将f的输出值的r比特作为输出分组2,然后整个输出值再输出到f中
- 反复执行获取所需长度的输出数据
双工结构
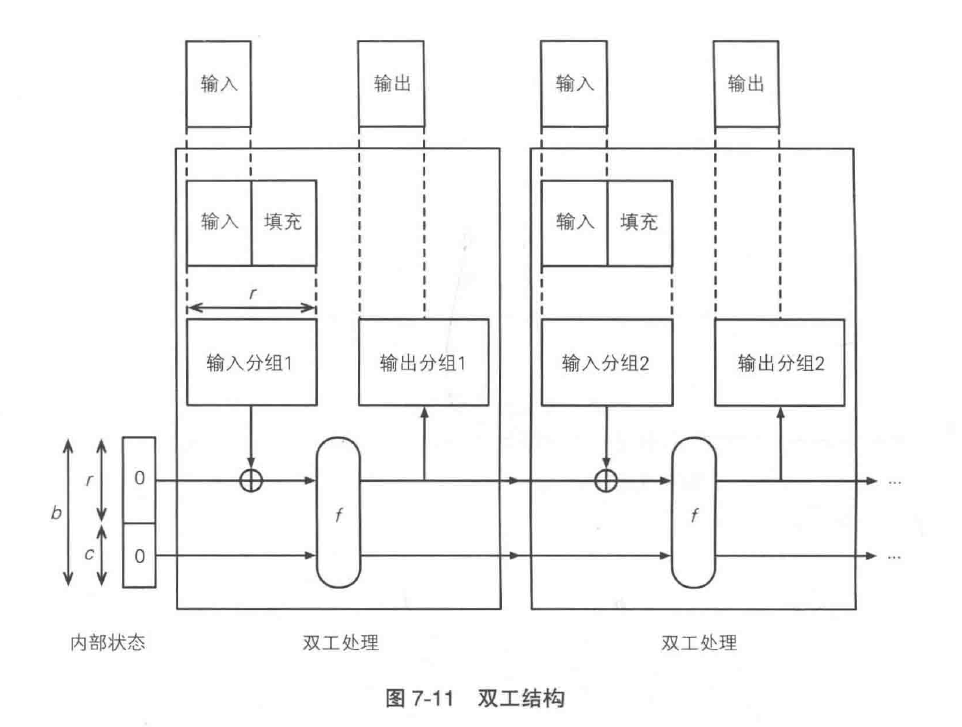
在海绵结构中,只能先吸收完毕之后才能输出。在双工结构里面输入和输出同时进行。发送和接受同时进行的方式称为全双工。
Keccak不仅可以用于计算散列值,还可以用于随机数生成器、留密码、认证加密、消息认证码。
Keccak的内部状态
Keccak的内部状态是三维的比特数组,如下图:
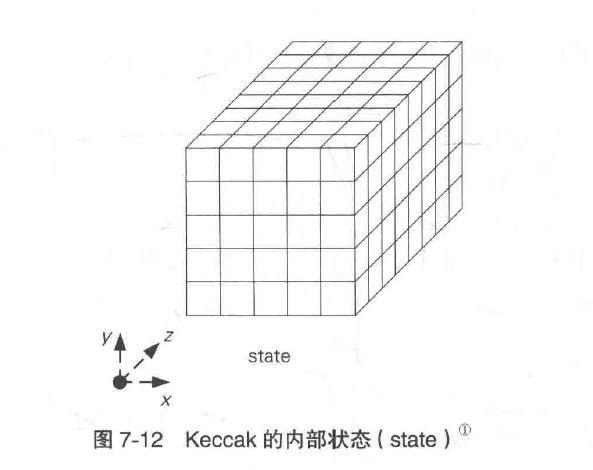
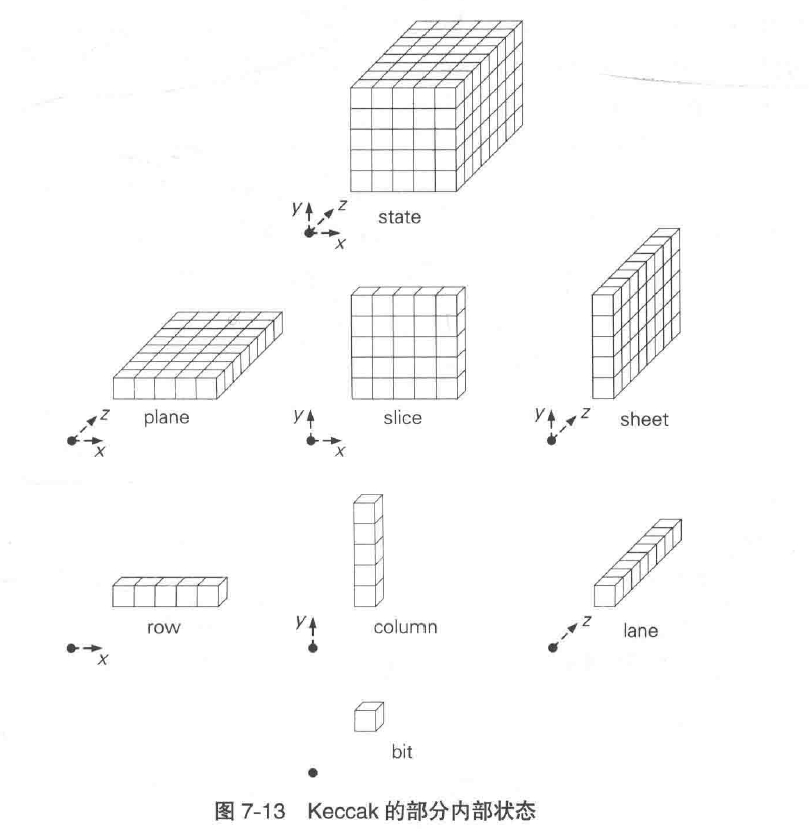
Keccak的本质就是实现将上述state进行搅拌的函数f。
函数Keccak-f[b]
b作为参数输入。b可以取25、50、100、200、400、800、1600
但是slice的大小始终是25.
无论b长度是多大,改变的只是lane的长度
Keccak-f[b]每一轮包含5个步骤,总共循环,12+2x轮。
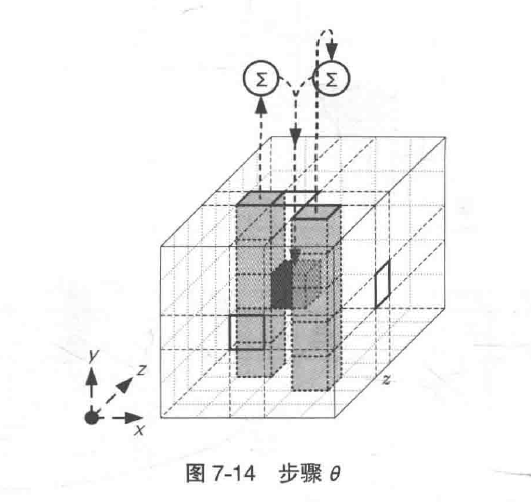
步骤θ
将位置不同的两个column中各自5bit通过XOR运算加起来,再与置换目标比特求XOR置换目标bit
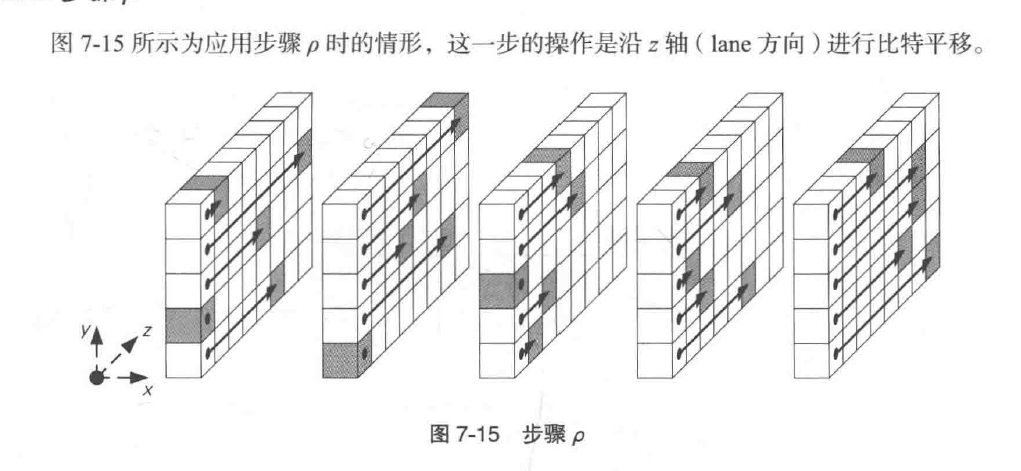
步骤ρ
沿着lane方向平移
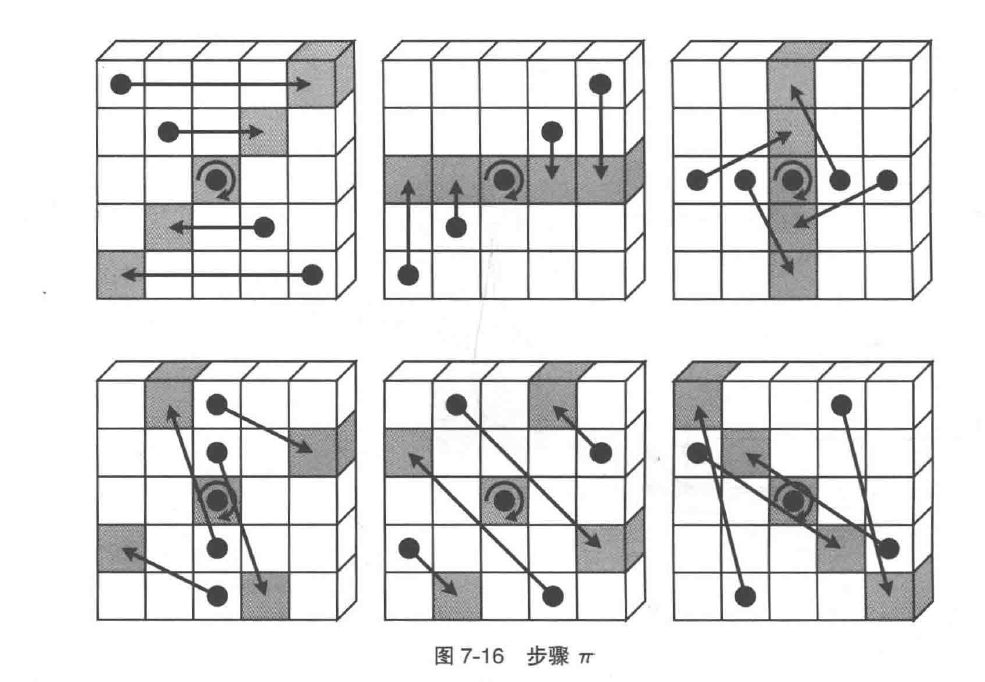
步骤π
整条lane上的slice进行如下操作
步骤χ
对输入比特取反,然后再取AND
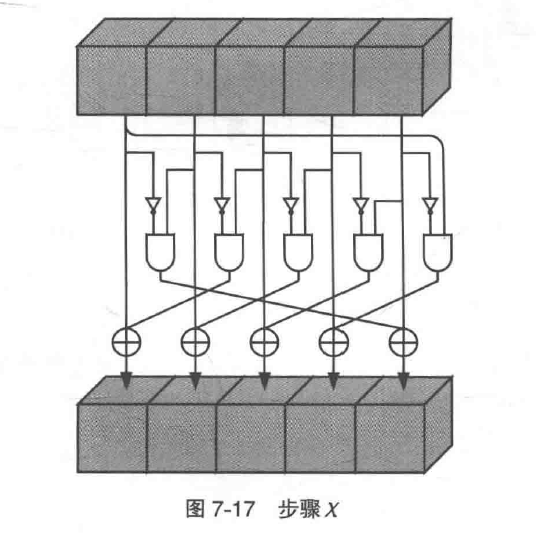
步骤ι
一个固定轮常数对整个state的所有比特进行XOR运算,使内部状态具备非对称性。
对Keccak的攻击
Keccak之前的单项散列函数都是通过循环执行压缩函数来生成散列值的,称为MD结构。
SHA-1、SHA-2都出现了理论可行的攻击方法,SHA-3使用了完全不同的海绵结构,所以之前的攻击方法是无效的。
缩水版Keccak的攻击竞赛
通过减少迭代论述、改变宽度b来进行攻击。因为结构清晰、易于分析,所以我们可以容易地对实际运用的标准算法进行强度评估。
应该使用哪种单项散列函数
- SHA-1只用于过去生成散列值的校验,不用于新用途
- SHA-2应对了针对SHA-1的攻击方法,安全可以使用
- SHA-3是安全的,可以使用
- 不应该使用任何自制算法
单项散列函数的攻击
单项散列函数无法解决的问题
单项散列函数能够识别出“篡改”但是无法辨别出“伪装”,也就是判断文件的拥有者。
需要认证就需要使用消息验证码和数字签名之类的技术。

