投币寄物柜的使用方法
硬币是关闭寄物柜的秘钥,钥匙则是打开寄物柜的秘钥。
本章学习内容
本章我们学习公钥密码
对称密码中,加密和解密密码相同,但是在公钥密码中,加密和解密密码不同。
秘钥配送问题
什么是秘钥配送问题
发送者将密文发给接受者,接受者必须拿到秘钥之后才能解密,这样就需要发送秘钥给接受者。
但是如果同时进行发送,则有可能被攻击者窃听。
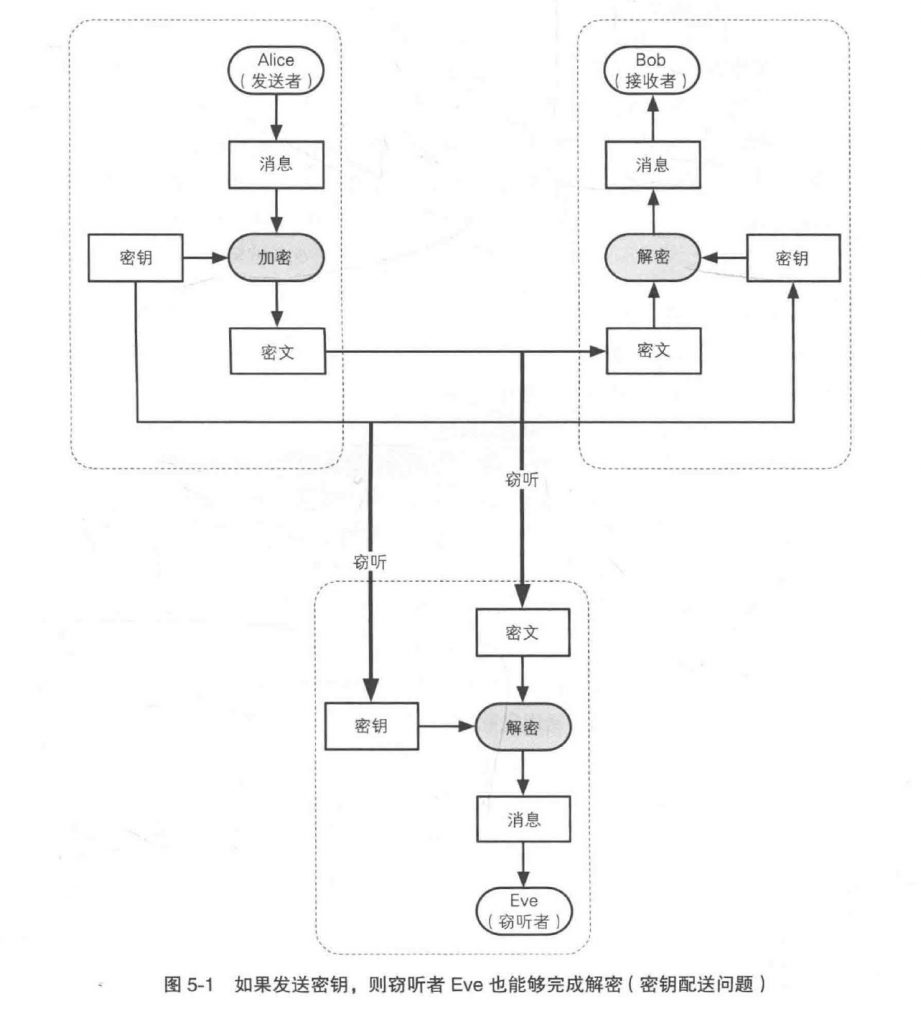
秘钥必须要发送,但是又不能发送,这就是秘钥配送问题
解决方法有以下几种:
- 通过事先共享秘钥
- 通过秘钥分配中心来解决
- 通过Diffie-Hellman秘钥交换来解决
- 通过公钥密码来解决
通过事先共享秘钥来解决
事先共享的问题是,如果人数很多的情况下需要准备巨大数量的秘钥。
例如一个公司内有1000个员工,则秘钥数量为1000 * 999 / 2 = 499500
通过秘钥分配中心来解决
每当员工入职时会为员工生成一个新的秘钥。
- Alice向秘钥分配中心发出希望与Bob通信的请求
- 秘钥分配中心通过伪随机数生成一个会话秘钥,这个秘钥是供Alice与Bob在本次通信中使用的临时秘钥
- 秘钥分配中心从数据库去除Alice与Bob的秘钥
- 秘钥分配中心使用Alice的秘钥对会话秘钥进行加密,发送给Alice
- 秘钥分配中心使用Bob的秘钥对会话秘钥进行加密发送给Bob
- Alice对来自秘钥中心分配中心的回话秘钥进行解密,得到会话秘钥
- Alice用会话秘钥对邮件进行加密并将邮件发送给Bob
- Bob对来自秘钥中心分配的会话秘钥进行解密,得到会话秘钥
- Bob用回话秘钥对来自Alice的密文进行解密
- Alice和Bob删除回话秘钥
秘钥分配中心有以下问题:
- 员工数量增加之后,负载会增加
- 如果秘钥分配中心瘫痪,则整个公司的加密通话都会瘫痪
- 如果攻击者对秘钥分配中心进行攻击,并且盗取秘钥库,后果会很严重
通过Diffie-Hellman秘钥交换来解决秘钥配送问题
通过Diffie-Hellman秘钥交换,加密通信的双方交换一些信息,但是即使被监听到也没关系
这个方法在11章讨论
通过公钥密码来解决秘钥配送问题
只需要发送公钥密码进行加密,接受者就可以用秘钥进行解密,不必害怕被窃听。
公钥密码
什么是公钥密码
公钥密码里面分公钥密码和私钥密码两种。
- 发送者只需要加密秘钥
- 接受者只需要解密秘钥
- 解密秘钥不可以被窃听者获取
- 加密秘钥被窃听者获取也没问题
公钥密码的历史
公钥通信的流程
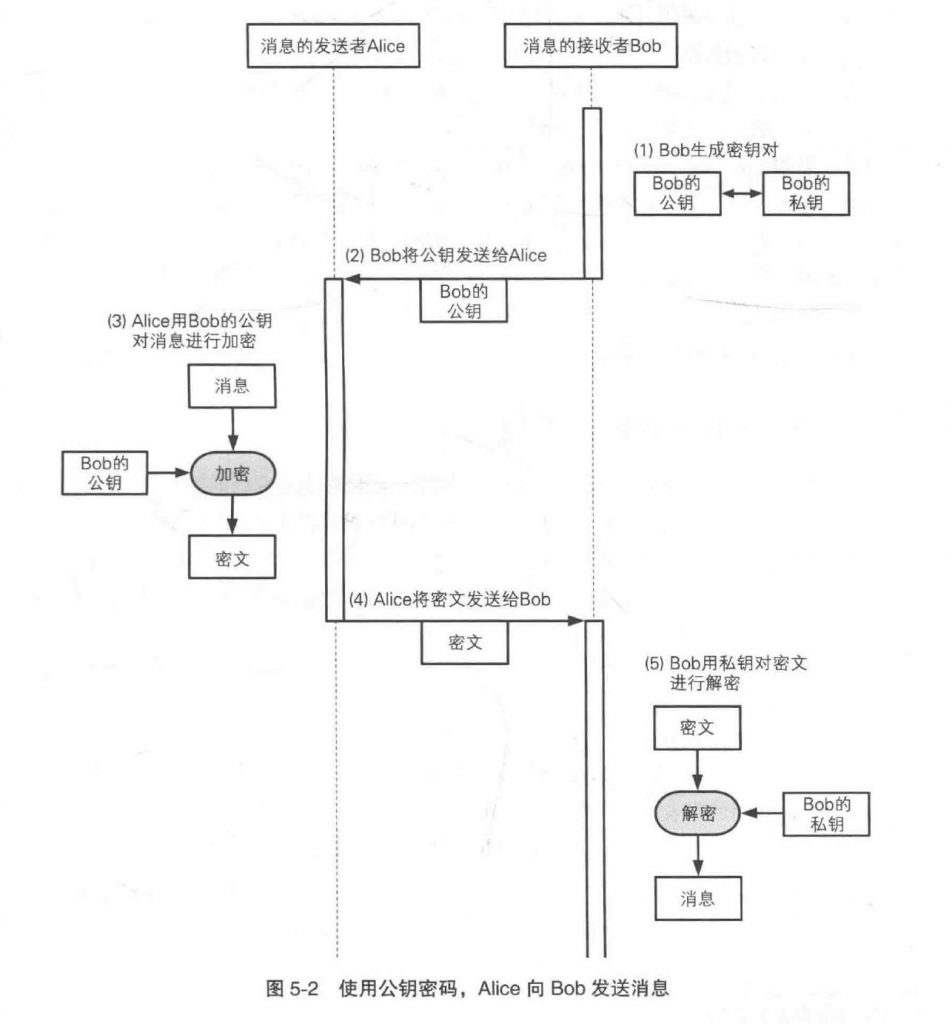
- Bob生成公钥和私钥,私钥由Bob自己保管
- Bob将公钥发送给Alice(无需保护)
- Alice用Bob的公钥对消息加密
- Alice将密文发给Bob
- Bob用私钥对密文解密
各种术语
非对称密码和公钥密码是同一个含义
私钥也有很多别名,个人秘钥、私有秘钥、非公开秘钥还有秘密秘钥
标准叫法就是私钥(private key)
公钥密码无法解决的问题
公钥配送的问题,公钥认证问题。窃听者可以通过进行中间人攻击来达到自己的目的。
还有一个问题就是处理速度只有对称密码的几百分之一。
时钟运算

加法
一般在加完之后取模就可以获得时钟加法的结果。
mod运算
使用mod代表取模运算
减法
乘法
实际上就是对乘法再进行mod
除法
乘法的逆运算,例如:

我们可以通过查表法计算
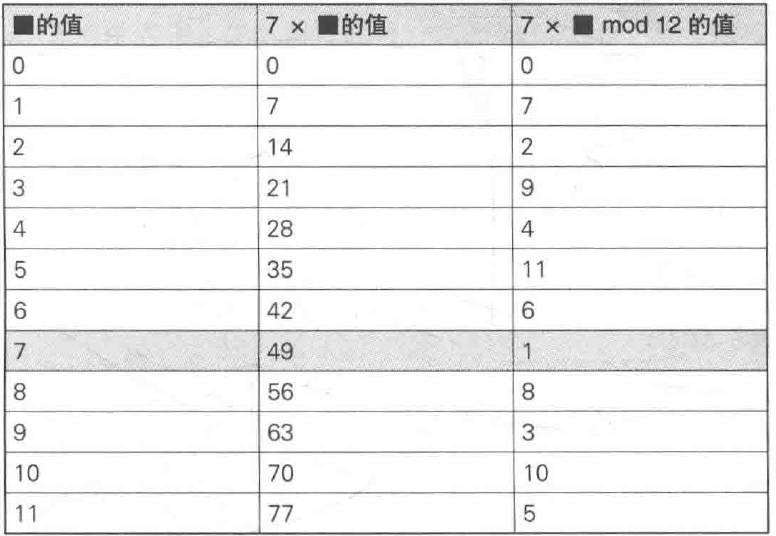
乘方
我们可以将中间步骤拆出来

两个小数的模取出来相乘再取模也是正确的。
对数
时钟运算中的对数称为离散对数,当数字很大的时候求对数非常困难。
从时钟指针到RSA
实际上RAS的加密与解密过程依赖了质因数分解的复杂性,就想离散对数的复杂性一样是,难以直接求解的。
RSA
什么是RSA
RSA由其三个开发者的名字首字母组成:Ron Rivest、Adi Shamir、Leonard Adleman。
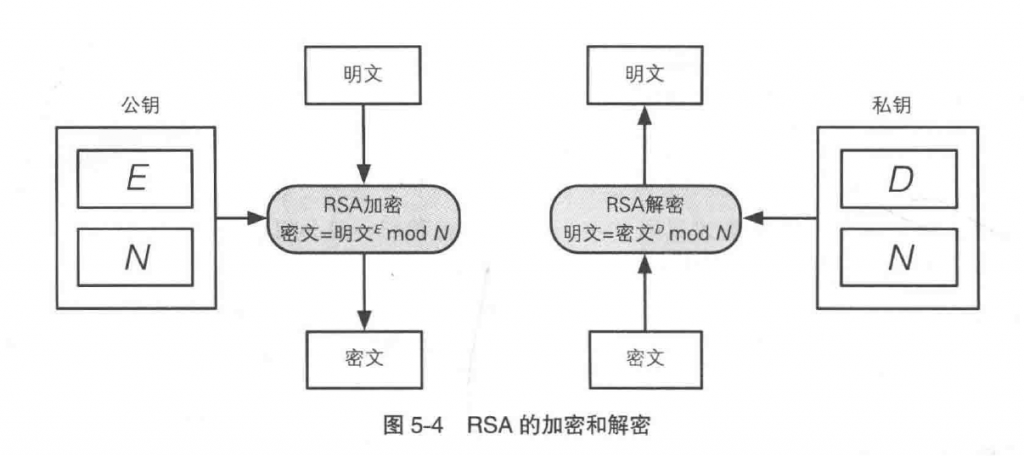
RSA加密
公式如下:
$密文=明文^E mod N$
E和N组合就是公钥。
RSA解密
公式如下
$密文=明文^D mod N$
D和N的组合就是私钥。
也就是密文和自己做D次乘法,再对其结果除以N求余数,就可以得到明文。
生成秘钥对
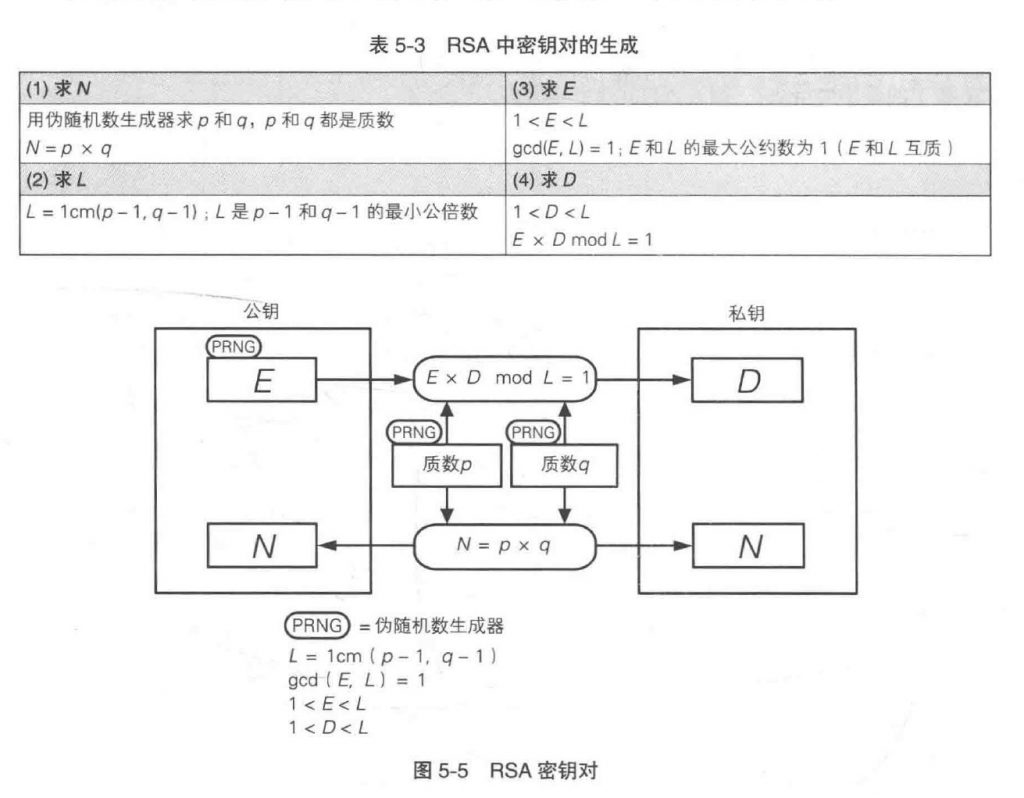
对RSA的攻击
密码破译者知道的信息:
密文、数E和N
密码破译者不知道的信息:
明文、私钥D、其他(破译者不知道的中间结果,p、q、L)
通过密文来求得明文
在对$明文^E$取了N的模之后计算将变得非常困难
通过暴力破解来找出D
我们可以逐一尝试有可能作为D的数字来破译RSA。但是D的长度变大难度就会变大。
RSA的p和q长度都是1024比特以上,N的长度在2048以上,2048比特以上的暴力破解是非常困难的。
通过E和N求出D
E x D mod L = 1
但是L是lcm(p-1,q-1)因为破译者不知道p和q所以不可能通过生成秘钥时相同的方式求出D。
RSA来说有一点非常重要,那就是质数p和q不能被密码破译者知道。把p和q交给密码破译者与把秘钥交出去没什么区别。
对N进行质数分解攻击
N=p x q 如果有高效的因数分解算法,RSA就可以被破解。
通过推测p和q进行攻击
因为p和q是伪随机数生成器生成的,所以如果使用了比较差的生成器就可能推测出p和q。
其他攻击
求D与对N进行质因式分解是否等价,这个问题需要数学方法来证明。
这样的方法还没有出现。
中间人攻击
攻击者混入发送者与接受者中间。
攻击者拦截接受者的公钥,发送自己的公钥。然后发送者使用攻击者的公钥进行发送信息,那么最终通话实际上是攻击者与发送者。
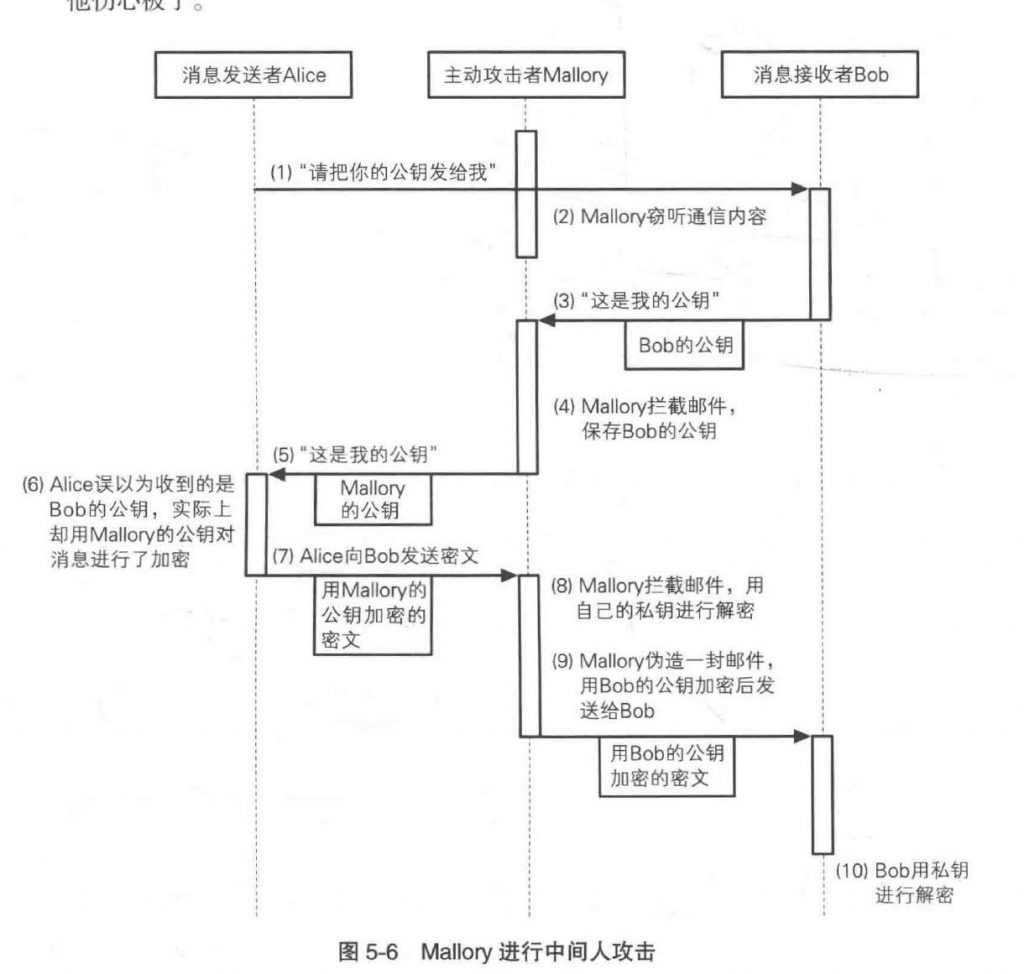
防御中间人攻击需要可通过**证书,**在第十章我们会讲到。
选择密文攻击
攻击者发送任意数据,服务器都会解密,并且返回结果,这个服务被称为解密提示。
在改进之后的算法RSA-OAEP中,会在明文前面填充一些认证信息,如果在解密后没有找到正确的认证信息就说明密文是由不知道明文的人生成的,会直接拒绝。
其他公钥密码
ElGamal方式
利用了mod N下求离散对数的困难度。
但是缺点是,加密后密文长度变成明文的两倍。
Rabin方式
利用了mod N下求平方根的困难度。
椭圆曲线密码
实际上是利用了通过将椭圆曲线上特定点进行特殊的乘法运算的逆运算复杂度来实现的。
关于公钥密码的Q&A
公钥密码的机密性
公钥密码比对称密码机密性是否更高:
无法回答,机密性高低与密码长度有关
公钥密码与对称密码的秘钥长度
秘钥长度为256比特的对称密码AES,比秘钥长度为1024比特的公钥密码RSA相比,安全性更高吗:
不是,不同密码种类的强度对比本身就不是一件容易的事情,很多时候会进行组合。
但是可以参考下表:
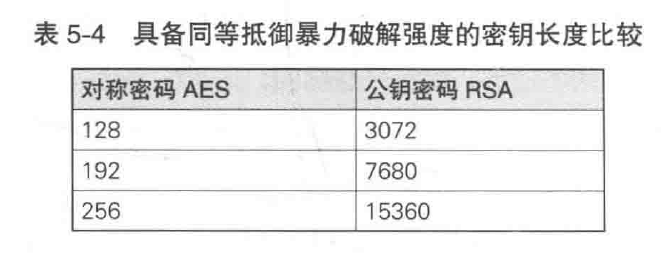
对称密码的未来
有公钥密码之后私钥密码会消失吗:
不会,各有优势。对称密码短,速度快,公钥密码可以解决配送问题。
RSA与质数
质数是否可能会被用光:
无需担心,512比特质数数量为10的150次方。每人每秒生成100亿个密钥对,那么100亿年后也只有10的39次方。
RSA与质因数分解
RSA加密中需要对大整数进行质因数分解吗?
不需要,在N求p、q时才会用到。
RSA的破译和大整数的质因数分解等价吗:
是等价的
RSA的长度
要抵御质因数分解,N的长度需要多少比特?
投入很大的计算资源的情况下1024已经能够分解了,但是2048还是安全的。
- 1024比特的RSA不应用于新用途
- 2048比特的RSA可在2030年前用于新用途
- 4096的RSA在2031年后依旧可以用于新用途

