【翻译】通过Unity学习PBR算法 ④

原文地址：http://www.jordanstevenstechart.com/physically-based-rendering

欢迎大家来我的小站：http://www.resetoter.cn/?p=592

组装你的PBR Shader Part2：几何阴影函数（The Geometric Shadowing Function）

什么是几何阴影函数（GSF）

几何阴影函数用于描述由于自身微表面投影行为产生的光的衰减。这种近似模型主要是为了模拟微表面之间的相互遮挡或者光线在多个微表面之间相互反射。在这些概率事件的影响下，当光线到达我们视线的时候必定会产生能量损失。为了精确地产生一个几何阴影函数我们必须采样器粗糙度来决定其微表面描述，虽然有很多种方法不包含粗糙度计算也能获得可信的阴影结果，但是它们远没有采用粗糙度的计算模型来得真实。

GSF是BRDF能量守恒的精华，如果没有GSF，BRDF可能会反射出比接收的光线更多的光照能量。微表面BRDF方程中有关键的一点是对于活跃区域（接收光照并且反射光线到视野的区域）和总区域的比例。

如果没有采用阴影和遮罩，那么活跃区域可能超过总区域，这将会导致BRDF函数在极端的数值情况下不符合能量守恒。

 float GeometricShadow = 1;

//the algorithm implementations will go here

 return float4(float3(1,1,1) * GeometricShadow,1);

为了预览我们的GSF函数，我们会将这个代码放在我们的NDF函数纸上，这种格式非常类似于我们之前对NDF函数的处理。

Impalicit GSF

经验模型是几何阴影渲染背后的基本逻辑。

float ImplicitGeometricShadowingFunction (float NdotL, float NdotV){
	float Gs =  (NdotL*NdotV);       
	return Gs;
}

通过将发现与光线的点乘和我们视觉方向与法线的点乘相乘，我们得到了一个比较精确地表面效果，并且这个表面效果能够通过我们视线变换而变换。

GeometricShadow *= ImplicitGeometricShadowingFunction (NdotL, NdotV);

Ashikhmin-Shirley GSF

设计用于各项异性的法线描述方程，Ashikhmin-Shirley GSF提供了一个不错的各项异性表现基础。

float AshikhminShirleyGSF (float NdotL, float NdotV, float LdotH){
	float Gs = NdotL*NdotV/(LdotH*max(NdotL,NdotV));
	return  (Gs);
}

由这个计算模型产生的微表面阴影非常微妙，就如上图所示。

eometricShadow *= ImplicitGeometricShadowingFunction (NdotL, NdotV);

Ashikhmin-Premoze GSF

这个阴影模型原本就是设计用于和各项同性的NDF进行配合的，不像Ashikhmin-Shirley 的方式。

float AshikhminPremozeGeometricShadowingFunction (float NdotL, float NdotV){
	float Gs = NdotL*NdotV/(NdotL+NdotV - NdotL*NdotV);
	return  (Gs);
}

GeometricShadow *= AshikhminPremozeGeometricShadowingFunction (NdotL, NdotV);

Duer GSF

Duer提出了这个GSF函数，解决了Ward GSF函数中发现的高光反射问题，Ward GSF我们在后面也会提到。Duer GSF产生了与Ashikhmin-Shirley非常相似的结果，但是它更倾向于用在各向同性的BRDF中，或者非常细微的各向异性BRDF上。

float DuerGeometricShadowingFunction (float3 lightDirection,float3 viewDirection, 
float3 normalDirection,float NdotL, float NdotV){
    float3 LpV = lightDirection + viewDirection;
    float Gs = dot(LpV,LpV) * pow(dot(LpV,normalDirection),-4);
    return  (Gs);
}

GeometricShadow *= DuerGeometricShadowingFunction (lightDirection, viewDirection, normalDirection, NdotL, NdotV);

Neumann GSF

Neumann GSF是另一种针对于各向异性法线描述的GSF。它产生了更明显的基于视线与光照方向的几何着色。

float NeumannGeometricShadowingFunction (float NdotL, float NdotV){
	float Gs = (NdotL*NdotV)/max(NdotL, NdotV);       
	return  (Gs);
}

GeometricShadow *= NeumannGeometricShadowingFunction (NdotL, NdotV);

Kelemen GSF

Kelemen GSF这种方式较为符合能量守恒。不像多数前面的模型，集合阴影的比例始终是常数，而是基于视角改变，这是一个非常近似于Cook-Torrance几何阴影着色方式的函数。

float KelemenGeometricShadowingFunction (float NdotL, float NdotV, 
float LdotV, float VdotH){
	float Gs = (NdotL*NdotV)/(VdotH * VdotH); 
	return   (Gs);
}

GeometricShadow *= KelemenGeometricShadowingFunction (NdotL, NdotV, LdotV,  VdotH);

Modified-Kelemen GSF

这是一个修改版的Kelemen函数。它通过将原来的做法修改为粗糙度来进行阴影描述。

float ModifiedKelemenGeometricShadowingFunction (float NdotV, float NdotL,
 float roughness)
{
	float c = 0.797884560802865;    // c = sqrt(2 / Pi)
	float k = roughness * roughness * c;
	float gH = NdotV  * k +(1-k);
	return (gH * gH * NdotL);
}

GeometricShadow *=  ModifiedKelemenGeometricShadowingFunction (NdotV, NdotL, roughness );

Cook-Torrance GSF

Cook-Torrance几何阴影函数是为了解决三种几何衰减的情况而创造出来的。第一种情况是光在没有被干涉的情况下进行反射，第二种是反射的光在反射完之后被阻挡了，第三种情况是有些光在到达下一个微表面之前被阻挡了。为了完全算出一下这些情况，我们使用下面列出的Cook-Torrance几何阴影函数来进行计算。

float CookTorrenceGeometricShadowingFunction (float NdotL, float NdotV, 
float VdotH, float NdotH){
	float Gs = min(1.0, min(2*NdotH*NdotV / VdotH, 
2*NdotH*NdotL / VdotH));
	return  (Gs);
}

GeometricShadow *= CookTorrenceGeometricShadowingFunction (NdotL, NdotV, VdotH, NdotH);

Ward GSF

Ward GSF是加强版的Implicit GSF。Ward用这种方式来加强法线描述函数。它非常适合用于突出当视角与平面角度发生改变后各向异性带的表现。

float WardGeometricShadowingFunction (float NdotL, float NdotV, 
float VdotH, float NdotH){
	float Gs = pow( NdotL * NdotV, 0.5);
	return  (Gs);
}

GeometricShadow *= WardGeometricShadowingFunction (NdotL, NdotV, VdotH, NdotH);

Kurt GSF

Kurt GSF又又又又是另一种各向异性的GSF，这个模型用于帮助控制基于粗糙度的各向异性表面描述。这个模型追求能量守恒，特别是切线角部分。

float KurtGeometricShadowingFunction (float NdotL, float NdotV, 
float VdotH, float roughness){
	float Gs =  NdotL*NdotV/(VdotH*pow(NdotL*NdotV, roughness));
	return  (Gs);
}

GeometricShadow *= KurtGeometricShadowingFunction (NdotL, NdotV, VdotH, roughness);

Smith Based Geometric Shadowing Functions

Smith Based GSF被认为比其他的GSF更加精确，并且考虑了粗糙度以及NDF的种类，这些函数需要处理两块数据以计算完整的GSF结果。

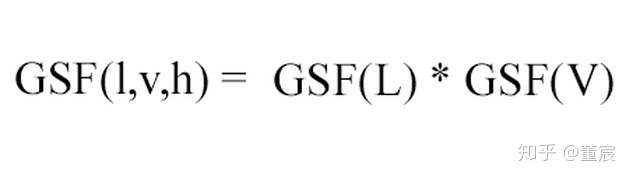
Walter et all. GSF

一般情况下GGX的GSF，[Walter et all](http://www.cs.cornell.edu/~srm/publications/EGSR07-btdf.pdf)创建了这个函数可以用于任意的微表面分布函数。Walter et al认为“**GSF对于BRDF形状的影响非常微小，除了在接近视线切线边缘或者非常粗糙的时候影响则会很大，但是不管怎么样，都需要保证能量守恒。**”在这个思想指导下，他们创建了一个符合这条原则的GSF公式，并且使用粗糙度来调整GSF的强度。

float WalterEtAlGeometricShadowingFunction (float NdotL, float NdotV, float alpha){
    float alphaSqr = alpha*alpha;
    float NdotLSqr = NdotL*NdotL;
    float NdotVSqr = NdotV*NdotV;

    float SmithL = 2/(1 + sqrt(1 + alphaSqr * (1-NdotLSqr)/(NdotLSqr)));
    float SmithV = 2/(1 + sqrt(1 + alphaSqr * (1-NdotVSqr)/(NdotVSqr)));


	float Gs =  (SmithL * SmithV);
	return Gs;
}

GeometricShadow *= WalterEtAlGeometricShadowingFunction (NdotL, NdotV, roughness);

Smith-Beckman GSF

最初是用于和Beckman微表面分布函数进行匹配的，Walter et al提出这也是适用于Phong NDF的GSF。

float BeckmanGeometricShadowingFunction (float NdotL, float NdotV, float roughness){
    float roughnessSqr = roughness*roughness;
    float NdotLSqr = NdotL*NdotL;
    float NdotVSqr = NdotV*NdotV;


    float calulationL = (NdotL)/(roughnessSqr * sqrt(1- NdotLSqr));
    float calulationV = (NdotV)/(roughnessSqr * sqrt(1- NdotVSqr));


    float SmithL = calulationL < 1.6 ? (((3.535 * calulationL)
 + (2.181 * calulationL * calulationL))/(1 + (2.276 * calulationL) + 
(2.577 * calulationL * calulationL))) : 1.0;
    float SmithV = calulationV < 1.6 ? (((3.535 * calulationV) 
+ (2.181 * calulationV * calulationV))/(1 + (2.276 * calulationV) +
 (2.577 * calulationV * calulationV))) : 1.0;


	float Gs =  (SmithL * SmithV);
	return Gs;
}

GeometricShadow *= BeckmanGeometricShadowingFunction (NdotL, NdotV, roughness);

GGX GSF

是对Walter et al模型的重构，是对Ndot/NdotV产生的GSF相乘得到的GSF。

float GGXGeometricShadowingFunction (float NdotL, float NdotV, float roughness){
    float roughnessSqr = roughness*roughness;
    float NdotLSqr = NdotL*NdotL;
    float NdotVSqr = NdotV*NdotV;


    float SmithL = (2 * NdotL)/ (NdotL + sqrt(roughnessSqr +
 ( 1-roughnessSqr) * NdotLSqr));
    float SmithV = (2 * NdotV)/ (NdotV + sqrt(roughnessSqr + 
( 1-roughnessSqr) * NdotVSqr));


	float Gs =  (SmithL * SmithV);
	return Gs;
}

GeometricShadow *= GGXGeometricShadowingFunction (NdotL, NdotV, roughness);

Schlick GSF

Schlick已经写了一系列对于SmithGSF的近似模型，并且可以使用在其他的Smith GSF。下面是最简单的对Smith GSF的近似模型。

float SchlickGeometricShadowingFunction (float NdotL, float NdotV, float roughness)
{
    float roughnessSqr = roughness*roughness;


	float SmithL = (NdotL)/(NdotL * (1-roughnessSqr) + roughnessSqr);
	float SmithV = (NdotV)/(NdotV * (1-roughnessSqr) + roughnessSqr);


	return (SmithL * SmithV); 
}

GeometricShadow *= SchlickGeometricShadowingFunction (NdotL, NdotV, roughness);

Schlick-Beckman GSF

这是Schlick对Beckman函数的近似。它通过对2/PI的平方根乘以粗糙度，而不是我们直接预计算出来的0.797884..来进行实现的。

float SchlickBeckmanGeometricShadowingFunction (float NdotL, float NdotV,
 float roughness){
    float roughnessSqr = roughness*roughness;
    float k = roughnessSqr * 0.797884560802865;


    float SmithL = (NdotL)/ (NdotL * (1- k) + k);
    float SmithV = (NdotV)/ (NdotV * (1- k) + k);


	float Gs =  (SmithL * SmithV);
	return Gs;
}

GeometricShadow *= SchlickBeckmanGeometricShadowingFunction (NdotL, NdotV, roughness);

Schlick-GGX GSF

Schlick对于GGX的近似实现，通过简单将我们的粗糙度除以2来进行模拟。

float SchlickGGXGeometricShadowingFunction (float NdotL, float NdotV, float roughness){
    float k = roughness / 2;


    float SmithL = (NdotL)/ (NdotL * (1- k) + k);
    float SmithV = (NdotV)/ (NdotV * (1- k) + k);


	float Gs =  (SmithL * SmithV);
	return Gs;
}

GeometricShadow *= SchlickGGXGeometricShadowingFunction (NdotL, NdotV, roughness);