原文地址:Jordan Stevens – Technical Artist
我的小站地址:【翻译】Write PBR Algorithms In Unity ③
组装你的PBR Shader Part1:微表面分布函数(高光函数)
什么是微表面分布函数(Normal Distribution Function)?
微表面分布函数是构成BRDF函数的是哪个核心要素之一。NDF统计学上描述了微表面发现的分布情况。在我们的使用当中,这个函数作为权重函数来缩放高光以及反射。将NDF看做表面的基础几何属性是非常重要的。让我们开始在我们的Shader中加一些算法,这样我们就可以看到NDF是怎么对我们的效果产生影响的了。
首先我们要做的就是编写一个算法,为了让这个算法可见,我们将我们返回的浮点数重写。
float3 SpecularDistribution = specColor;
//the algorithm implementations will go here
return float4(float3(1,1,1) * SpecularDistribution.rgb,1);之后的一些计算环节也会按照这样的形式出现,当你在计算环节中写完了算法,你会在当前位置写上算法。如果你要写一个新的算法的时候简单将其注释掉就完事儿了,结果只会基于没有注释的算法。别担心,我们会将这种做法改进,以在Unity中更轻松地切换不同的算法,再也不用进行注释惹。
让我们从最简单的blinn-phong算法开始:
Blinn-Phong NDF

Blin近似算出了Phong高光,并将其作为Phong高光模型的优化版。
Blin通过半角向量与法向量点乘显然比计算光的反射方向要快。这个算法算出来的结果要比Phong更加柔和。
float BlinnPhongNormalDistribution(float NdotH, float specularpower, float speculargloss){
float Distribution = pow(NdotH,speculargloss) * specularpower;
Distribution *= (2+specularpower) / (2*3.1415926535);
return Distribution;
}Blin-Phong算法并不符合物理规律,但是依旧可以产生可信的高光,用于一些特殊的美术用途。将上面的算法放入算法阶段,并且将下面的代码放入到片元阶段。
SpecularDistribution *= BlinnPhongNormalDistribution(NdotH, _Glossiness, max(1,_Glossiness * 40));如果你往你的shader中输入一个光滑度你会看到物体会有一个高光来表现其法线分布,而剩下的地方都是黑色。这样我们可以更轻松地调试我们的shader。上方代码中的40只是我能够让函数提供更大的范围,但是对每个人来说并不是一个确定的值。
Phong NDF

float PhongNormalDistribution(float RdotV, float specularpower, float speculargloss){
float Distribution = pow(RdotV,speculargloss) * specularpower;
Distribution *= (2+specularpower) / (2*3.1415926535);
return Distribution;
}Phong算法是另外一种非物理算法,但是它产生比Blin近似出更好的效果。下面是实现的例子:
SpecularDistribution *= PhongNormalDistribution(RdotV, _Glossiness, max(1,_Glossiness * 40));为了与Blin-Phong进行对比,不要过于在意40这个值。
Beckman NDF

Beckman微表面分布函数是一个更加高级的函数,并且将我们的粗糙度带入计算当中。粗糙度和法线与半角向量的点乘共同对物体表面的法线分布进行近似。
float BeckmannNormalDistribution(float roughness, float NdotH)
{
float roughnessSqr = roughness*roughness;
float NdotHSqr = NdotH*NdotH;
return max(0.000001,(1.0 / (3.1415926535*roughnessSqr*NdotHSqr*NdotHSqr))
* exp((NdotHSqr-1)/(roughnessSqr*NdotHSqr)));
}该函数的实现非常简单。
SpecularDistribution *= BeckmannNormalDistribution(roughness, NdotH);在Beckman光照模型处理物体表面的时候需要注意的一点是。你可以从上面的图像中看出,Beckman光照模型随着光滑度的变化在慢慢变化,直到一个高光点聚拢在了一个确定的点上。当表面的光滑度增加的时候反射高光聚拢在了一起,产生了非常不错的从粗糙到光滑的艺术效果。这种表现效果在早期的粗糙材质中非常受欢迎,对于塑料中光滑度的渲染也非常不错。
Gaussian NDF

Gaussian NDF不像其他的一些计算模型那样受欢迎,因为它倾向于渲染出更柔和的反射高光,而不是渲染光滑度更高的材质。对于艺术效果来说是可行的,但是对于它是否更符合自然物理还存在着争论。
float GaussianNormalDistribution(float roughness, float NdotH)
{
float roughnessSqr = roughness*roughness;
float thetaH = acos(NdotH);
return exp(-thetaH*thetaH/roughnessSqr);
}这个算法的实现与其他的NDF非常相似,都是依赖于粗糙度以及表面发现于半角向量的点乘。
SpecularDistribution *= GaussianNormalDistribution(roughness, NdotH);GGX NDF

GGX是最受欢迎的光照模型之一,当前大多数的BRDF函数都依赖于它的实现。GGX是由Bruce Walter和Kenneth Torrance发表出来的。在他们[论文]中的许多算法都是目前大量被使用到的。
float GGXNormalDistribution(float roughness, float NdotH)
{
float roughnessSqr = roughness*roughness;
float NdotHSqr = NdotH*NdotH;
float TanNdotHSqr = (1-NdotHSqr)/NdotHSqr;
return (1.0/3.1415926535) * sqr(roughness/(NdotHSqr * (roughnessSqr + TanNdotHSqr)));
}SpecularDistribution *= GGXNormalDistribution(roughness, NdotH);The specular highlight of the GGX Algorithm is very tight and hot, while still maintaining a smooth distribution across the surface of our ball. 这是一个简单的例子来解释为什么GGX算法经常将反射率变换为金属度来表示。
Trowbridge-Reitz NDF

Trowbridge-Reitez方法在GGX相同的论文中被发表出来。主要可见的区别就是物体边缘的高光比GGX的方式产生的锐利边缘要更加柔和了。
float TrowbridgeReitzNormalDistribution(float NdotH, float roughness){
float roughnessSqr = roughness*roughness;
float Distribution = NdotH*NdotH * (roughnessSqr-1.0) + 1.0;
return roughnessSqr / (3.1415926535 * Distribution*Distribution);
}类似地,Trobridge-reitz方法也依赖于粗糙度与半角向量和法线的点乘。
SpecularDistribution *= TrowbridgeReitzNormalDistribution(NdotH, roughness);Trowbridge-Reitz Anisotropic NDF

各向异性的NDF方程产生了各向异性的表面描述。它允许我们做出有各项异性效果的表面。这个函数我们需要添加一个新的属性来确定各向异性的强度。
我们的属性
_Anisotropic("Anisotropic", Range(-20,1)) = 0我们的变量
float _Anisotropic;float TrowbridgeReitzAnisotropicNormalDistribution(float anisotropic, float NdotH, float HdotX, float HdotY){
float aspect = sqrt(1.0h-anisotropic * 0.9h);
float X = max(.001, sqr(1.0-_Glossiness)/aspect) * 5;
float Y = max(.001, sqr(1.0-_Glossiness)*aspect) * 5;
return 1.0 / (3.1415926535 * X*Y * sqr(sqr(HdotX/X) + sqr(HdotY/Y) + NdotH*NdotH));
}各向异性的材质与各向同性的材质的其中一个区别是是否需要使用切线或者副法线来描述表面。上图表现出来的是各向异性为1时的效果。
SpecularDistribution *= TrowbridgeReitzAnisotropicNormalDistribution(_Anisotropic,NdotH,
dot(halfDirection, i.tangentDir),
dot(halfDirection, i.bitangentDir));Ward AnisoTropic NDF
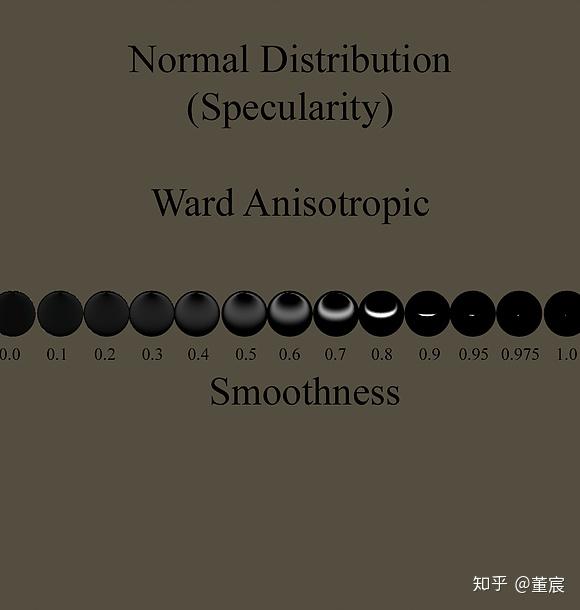
Ward方式的各向异性BRDF函数产生了与上一个方式不同的效果。其高光变得更加柔和,随着光滑度的降低高光液消失得更快了。
float WardAnisotropicNormalDistribution(float anisotropic, float NdotL,
float NdotV, float NdotH, float HdotX, float HdotY){
float aspect = sqrt(1.0h-anisotropic * 0.9h);
float X = max(.001, sqr(1.0-_Glossiness)/aspect) * 5;
float Y = max(.001, sqr(1.0-_Glossiness)*aspect) * 5;
float exponent = -(sqr(HdotX/X) + sqr(HdotY/Y)) / sqr(NdotH);
float Distribution = 1.0 / (4.0 * 3.14159265 * X * Y * sqrt(NdotL * NdotV));
Distribution *= exp(exponent);
return Distribution;
}就像Trowbridge-Reitz函数,Ward函数也需要切线与副法线(切线)数据,而且依赖于光与法线的点乘和视觉方向与法线的点乘。
SpecularDistribution *= WardAnisotropicNormalDistribution(_Anisotropic,NdotL, NdotV, NdotH,
dot(halfDirection, i.tangentDir),
dot(halfDirection, i.bitangentDir));
